今回は数ⅠAの式の展開を超わかりやすく解説します。この記事だけで式の展開は一発です。
展開にはおおきく分けて以下の2つがあると思ってください。
今回はこれらをそれぞれ解説していきます。
①展開公式を用いた展開
教科書には「展開公式」というものが載っています(別名:因数分解公式)。まずはそれらを一か所にまとめたものを次に示します。
2次の展開公式
① \((a+b)²=a²+2ab+b²\)
\((a-b)²=a²-2ab+b²\)
② \((a+b)(a-b)=a²-b²\)
③ \((x+a)(x+b)=x²+(a+b)x+ab\)
3次の展開公式
④ \((a+b)³=a³+3a²b+3ab²+b³\)
\((a-b)³=a³-3a²b+3ab²-b³\)
⑤ \((a+b)(a²-ab+b²)=a³+b³\)
\((a-b)(a²+ab+b²)=a³-b³\)
これらさえ頭に入れておけば良いのですが、この式を丸暗記するだけではもちろんダメです。公式は使えないと意味がありません。この式を覚えても、試験などで使えなければ無意味なのです。
ということで、これらの公式を使うために覚えるにはどうしたらよいのか、具体的な考え方を説明していきます。
aやbには他の文字や数字も入る
aやbといった文字が公式に入っていますが、これらの文字は数字の代わりであり、aやbである必要はありません。何が言いたいかというと、「aやbには基本的に違う文字・数字が入るぞ!」という意識で向き合うということです。
たとえば、②の\((a+b)(a-b)=a²-b²\)は、「和と差の積は2乗引く2乗」のように覚えてみるとよいでしょう。このように覚えることで、この公式に当てはまる形が出てきた時に気づく確率がぐんと上がります。式を言葉にして覚えるのはとても有効です。
使って覚えるのがはやいし確実
公式を眺めて覚えようとする人がいますが、めちゃくちゃに非効率です。どのような公式もそうですが、使いまくって覚えるのが一番早いです。
問題の経験を積む
使って覚えることで経験した問題が増えていきます。一度経験しているだけで正答率は跳ね上がります。同じような問題ばかりではなく、様々な問題を解いてみましょう。(自分のレベルにあった問題を解いて下さい)
頭を使わなくなる
使って覚えると、段々頭を使わずに解けるようになってきます。こうなってしまえば完全に身についていると言えます。式の展開・因数分解はこのレベルまで上達しないと入試問題などの難しい問題は解くのが難しいでしょう。
このあたりの話を詳しくしている記事もあるので是非見てみてください。
また、このあたりの感覚の話は文字で伝えるのに限界があるのでYouTubeで学ぶことをおすすめします。下にこの回の動画を載せておきます。
②一般的な展開
一般的な展開とは展開公式を使わない展開のことです。
展開は必ずできるので、展開公式を使えないときは地道に展開しましょう。
展開の脳内イメージ
展開するときの脳内イメージは次の通りです。カッコの中のすべての項から他方のカッコの中のすべての文字に対して線を伸ばします。あとは線でつながれた項をかけて、出てきたものをすべて足して終わりです。それぞれの色の線で結ばれた項の積が同じ色の下線で示されています。
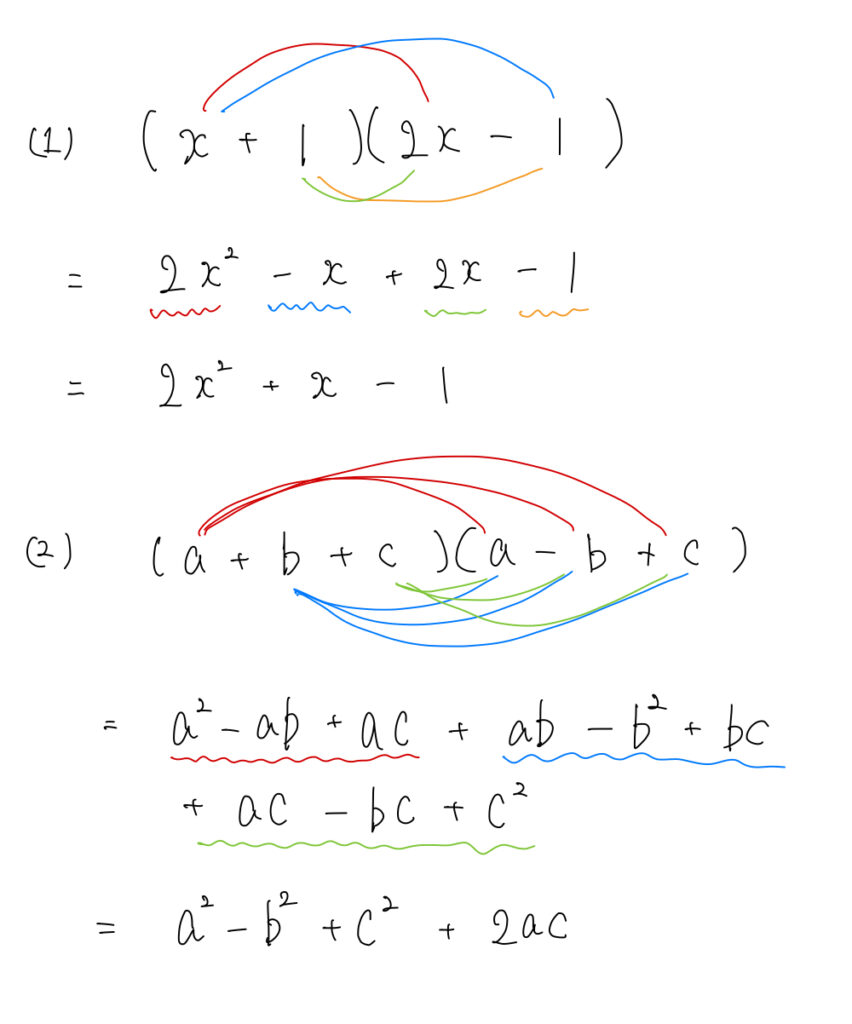
カッコが増えてもそのうち2つカッコを選んで同じように計算すればその2つのカッコは1つのカッコに入るのであとはそれを繰り返せば展開できます。
同類項を意識して計算速度をあげよう
展開をするときに、掛け算で出てくる項の文字の部分を考えて、展開と同時に同類項をまとめれば計算スピードがアップします。
共通テストでは計算スピードがかなり大事なので早いうちにこの省略法に慣れておきましょう。
展開公式は最悪知らなくても展開は可能
①で説明した展開公式が使えなかったら②の一般的な展開と説明しましたが、実は最初から②でやっても100%展開はできます。
しかし、もちろん知らないと相当な不利益が生じます。
計算が非効率になる
展開公式を知っていれば一瞬で計算できるものに時間がかかってしまいます。
この理由だけでも展開公式を身に着ける価値はあるでしょう。
因数分解では必須
このすぐ後の章で出てくる「因数分解」の単元では「因数分解公式」というものが出てきますが、展開公式と全く同じです。それもそのはず、因数分解とは展開の逆の操作です。
その因数分解に、因数分解公式(展開公式)が必須なのです。なので、絶対に展開公式はマスターしておきましょう。








コメント