因数分解をするとき、知っておくと便利なのが「たすき掛け」です。
今回はそのたすき掛けについてどこよりも詳しく解説していきます。
たすき掛けとは?そもそもいつやるの?
たすき掛けとは、2次の整式を因数分解するために用いる手法の一つです。
ある操作をすることで、因数分解後の係数を特定することができます。
たすき掛けは、2次の項の係数が1でない2次の整式を因数分解したいときに使います。
詳しい使いどころは下のリンクから飛べる記事で解説しているので知りたい方は是非ご覧ください。
たすき掛けの基本手順
それではさっそく基本的な手順を解説していきます。
① 2次の整式の係数を【2次⇒定数項⇒1次】の順に並べて書く
例を挙げます。例えば、下記のような2次の整式を因数分解したいとします。
\(2x²+7x+3\) ⇐因数分解したい!
この場合、「2 3 7」と書きます。これで準備完了です。
ちなみにたすき掛けの途中式は一切解答に記述する必要はないのでどこか空いているスペースに書きましょう。
② かけて左側の2つの数字になる2つの整数をそれぞれ考える
先ほどの例を用いて説明します。
左側の2つの数字とはこの場合2と3のことです。つまり、かけて2になる2つの数字、かけて3になる2つの整数をそれぞれ見つければOKです。
この例の場合、
2=2×1
3=3×1
しか整数の組み合わせはありません。(正の数の場合は負×負のパターンは考えなくてよいです。)
③ 見つけた数字をたすき掛けして左側の数字を作る
これも例で説明します。
文章だけでは伝わりづらいので、次に図解を示します。
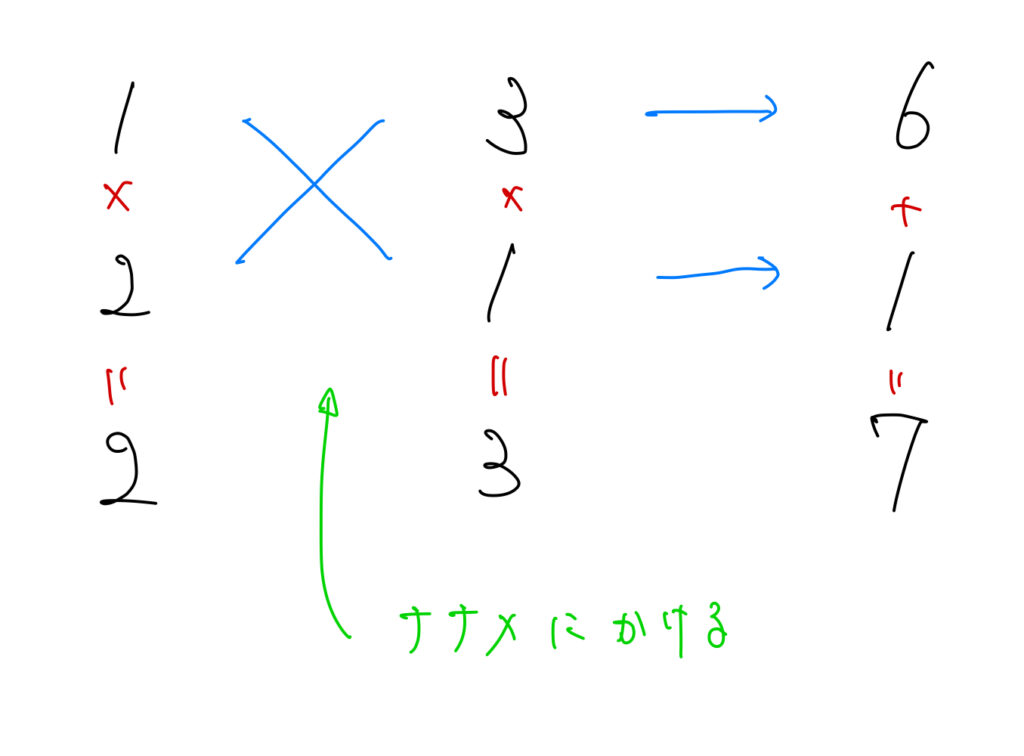
このようなイメージで最初左に書いた数字を作っていきます。
④ できた数字のペアをかっこでくくって因数分解完了
③で、左側にできた2ペアが因数分解した形になっています。下に図を示します。

これで手順は終了です。続いてこの手順を踏むにあたってのコツを説明します。
たすき掛けのコツ
基本的な手順はここまでで説明してきました。それに加えて、たすき掛けをスムーズに行うためのコツを解説していきます。
① 最初は符号を考える
最初に考えるのは符号です。次の例で考えてみましょう。
例題) \(2x²-5x-3\)
この場合、次のように考えていきます。
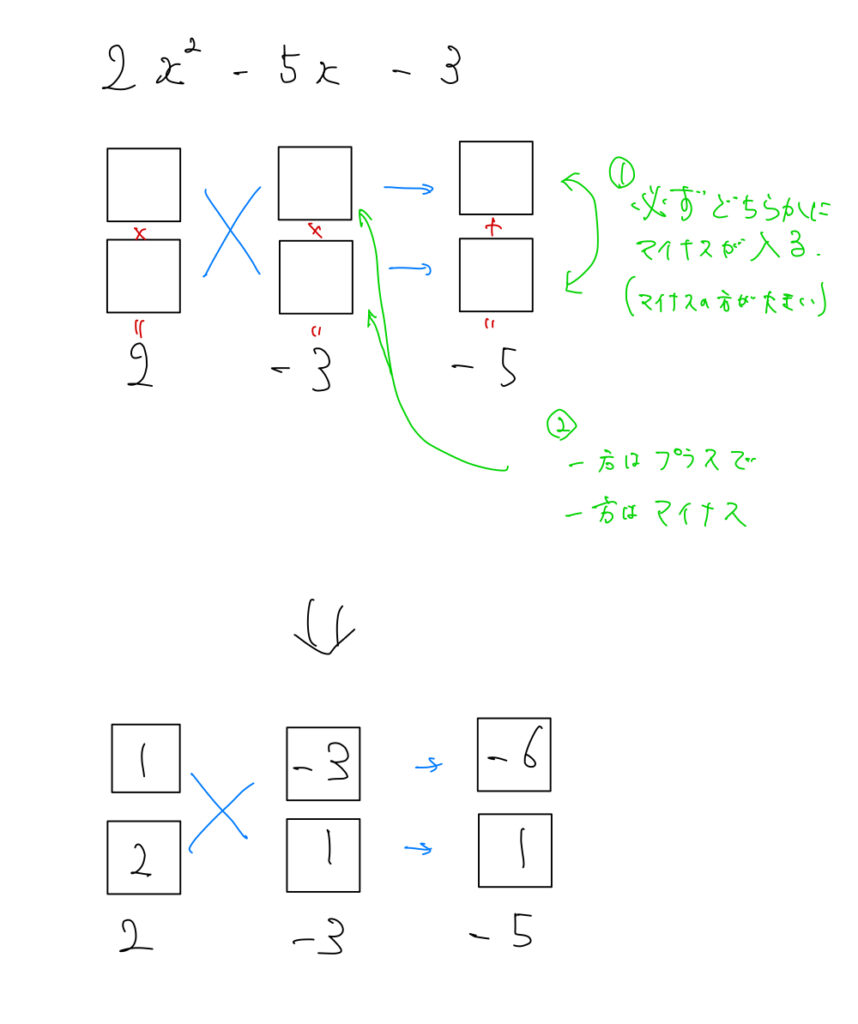
このようにすることでかなり効率よく候補を絞ることができます。
② 掛け算を構成する数字から考えること
たすき掛けには、縦に掛け算をする左側の2ブロックと、縦に足し算する右側の1ブロックがありましたよね。このとき先に考えるのは掛け算の方です。理由は掛け算の方が足し算よりも圧倒的に数字の組み合わせが少ないからです。掛け算の方で候補を絞ってから足し算に当てはめてみましょう。
最後に
たすき掛けは使いこなせるようになればかなり有効な計算方法です。何度も繰り返し練習して自分のものにしましょう!






コメント